Can I Test For Broken Strands?
Over the years, numerous Cirris customers have asked us if there was a way to detect broken strands in their cables by using standard Cirris cable testers? If you have ever seen a cable assembly with broken wire strands or strands outside of a crimp, it would seem reasonable to assume that normal resistance testing would uncover these faults (or would it?). With such obvious visible defects, shouldn’t your cable/harness tester easily find these kinds of problems? The results might surprise you!


Test This! – The Empirical Results
The Setup
We used:
- A 38″ length of 7 stranded, 26 AWG wire.
- An HP 34401A multi-meter capable of measuring resistance down to 1/10,000th of an ohm using 4-Wire (Kelvin) measurements.
- A Dino-Lite Digital Microscope.
We measured the end-to-end resistance of a 38″ wire to establish a baseline resistance. We then cut one strand at a time and took the resulting resistance readings after each strand was cut. After recording each reading we moved our Dino-Lite Digital Microscope over the wire and took an image (the images in the table below are from that microscope).
Of particular note are the experiments we did after five wires were cut (we “warmed” the cable slightly) and after all wires were cut (we “mushed” all the wires back together). Notice the effects below.

Wire Image | 4 Wire Measurement | Condition of Wire |
 | 00.1290 | No strands are cut |
 | 00.1290 | One strand has been cut |
 | 00.1291 | Two strands have been cut |
 | 00.1294 | Three strands have been cut |
 | 00.1293 | Four strands have been cut |
 | 00.1297 | Five strands have been cut |
 | 00.1334 | With Five strands cut we decided to experiment. We warmed up about 8" of the wire by holding it in our hands to see how it would effect the resistance readings. |
 | 00.1320 | Six strands have been cut. |
 | 00.1351 | All Seven strands have been cut, but we then simply smoothed down the wires with our fingers and pushed the two ends together to take our last reading. |
What have we learned?
Our baseline resistance (all wires intact) is 0.1290 Ω (129 milli ohms). The resistance measured when all but one strand was cut is 0.1320 Ω (132 milli ohms)–a difference of only 3 milliohms! What can we compare that amount of resistance to for a sense of comparison? When we measured the resistance with 5 strands cut we got 0.1297 Ω. When we held about 8″ of the wire in our hands to warm it up we got a measurement of 0.1334 Ω–a difference of 3.6 milliohms. We actually got more ohms of resistance change when we held a small portion of the cable than we did when we cut all but one strand of the 7 stranded wires! Remarkable!
Another comparison:
How long would the cable have to be in order for the difference of 0.0030 Ω (no strands cut vs. all but one strand cut) to be absorbed by the change in length? Here are the calculations: 0.0030 divided by 0.0034 (resistance of 1″ of 26 gauge wire) = 0.882″ or nearly 0.9″. So, if your cable were 0.9″ longer you would easily absorb the 0.0030 Ω difference between “no strands cut” to “all strands cut but one.” Note what variations in wire length your specs allow.
Yet Another comparison:
Manufacturer’s specs on cross-sectional variation in stranded wire construction show us that plus or minus 2% is the nominal allowable variation. So, if you take 2% of 0.1290 Ω (which you will remember is the resistance measured with all strands un-cut on our 38″ piece of wire) you get 0.00258 Ω or just under the 0.003 Ω which is the same variation as our “uncut strands vs all strands cut but one.” It appears that this 0.0030 Ω number we have been talking about may honestly be described as the “noise number” for this cable.
It has become evident that trying to find broken wire strands in your cable is not practical even using 4-wire Kelvin measurements on equipment that can measure down to 1/10,000th of an ohm. The variation in wire length, cross-sectional measurement and room temperature swamp the resistance variance found in broken wire strands. Sorry, it’s physics!
Want to better understand the Theoretical model behind the Empirical data? Read on below.
The Theoretical
A cable is made up of a number of smaller gauge wires:

In this example, our cable is 38 inches long and is made of 7 strands of copper wire that are roughly 34 AWG.

The resistance of 34 AWG copper wire is 0.2609 ohms/ft. at room temperature.
The resistance of each strand is parallel to the resistance of all the other strands, or in other words, the total resistance of the cable is the parallel resistance of all the strands.
Parallel resistance is figured using the formula below:
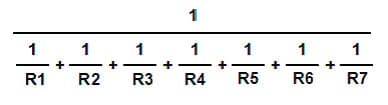
In our theoretical cable, the resistance is: 0.1180262 ohms.
Let’s suppose we have a broken strand and the gap made by the broken strand is 0.005 inches.
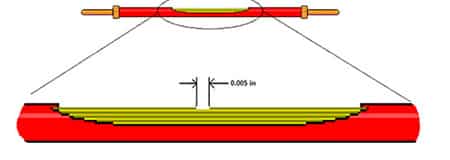
Now, our cable is 6 parallel paths for 0.005 inches that is in series with 7 parallel paths that are 37.995 inches long.
The 0.005 gap is 1/7600th of the length of the cable.

The resistance of 6 strands for a length of 38 inches is 0.1376972 ohms. Divide this by 7600 and you get the resistance of 6 parallel strands over a length of 0.005 inches or 0.0000181 ohms. This little bit of resistance is in series with our 7 parallel paths that are 37.995 inches long.
This 37.995 inches is 7599/7600th of our length or 0.999868 of 38 inches. Our original resistance of 0.1180262 ohms for 38 inches times 7599/7600 gives us 0.1180106 ohms for 37.995 inches.
Series resistance simply add up so the total resistance of our cable with the broken strand is: 0.0000181 ohms + 0.1180106 ohms giving us a total of 0.1180287 ohms.
The difference in resistance for the two conditions (0.1180262 ohms for no broken strand vs. 0.1180287 for one broken strand) is 2.58 micro ohms or 0.00000258 ohms.
We think you will agree that this is too small to measure in any kind of real-world scenario, and very difficult to measure even in a laboratory environment!

